基本正则引擎的实现

发表于   |  

介绍

　　这个篇文章是对我的一个基本功能的正则引擎的实现过程的大致介绍与讨论，实际上在之前的文章中我已经对正则引擎的实现有所涉及，当时是翻译了有关Thompson NFA的文章，文章及其附带的源代码中已经对如何实现一个简单的正则引擎有了详细的说明，但是该文章对正则引擎的介绍并不深入，同时实现方式也过于简单化，虽然最终的结果是高效可靠的，但是这个实现不便于扩展，同时支持的功能也比较有限，因此在这一次的实现中，我采用了更加主流的方法，这样支持了更多的功能，同时也易于扩展。该项目使用的语言为C++，完整项目请移步regexEngine2。

引擎功能介绍

下面简单地介绍一下这一次的正则的一些功能(并联串联功能不再赘述)：

1.’*‘：零个或多个

2.’+’：一个或多个

3.’?’：零个或一个

4.’ . ‘：匹配任意一个字符

5.{a}：重复a次；{a,b}：重复次数大于等于a小于等于b；{a,}：重复次数大于等于a

6.[m-n]：匹配范围内的字符(例如：[a-g]等价于a|b|c|d|e|f|g等价于[abcdefg])

7.[^m-n]：匹配不是范围内的字符

同时还加入了一些特殊的转义字符：

1.\d：等价于[0-9]

2.\D：等价于[^0-9]

3.\s：等价于[\t\n\r\f]

4.\S：等价于[^\t\n\r\f]

5.\w：等价于[a-zA-Z0-9_]

6.\W：等价于[^a-zA-Z0-9_]

　　由此可见，这一次的正则引擎的功能相较于之前的实现有了更多的加强，这样一来使得正则匹配更加方便易用，但就如同我刚开始说的，这也仅仅是一个基本的功能，因为真正工业级别的正则引擎还有许多高级但是实用的功能，例如：贪婪匹配与非贪婪匹配(其实这个实现起来比较简单)，正向预查，反向预查等等，这些功能使得正则表达式更加强大，但是实现起来也更加的复杂，由于我的本意并不是做一个完备的正则引擎，因此这些高大上的功能就跳过。下图大致展示了程序匹配时的情况：

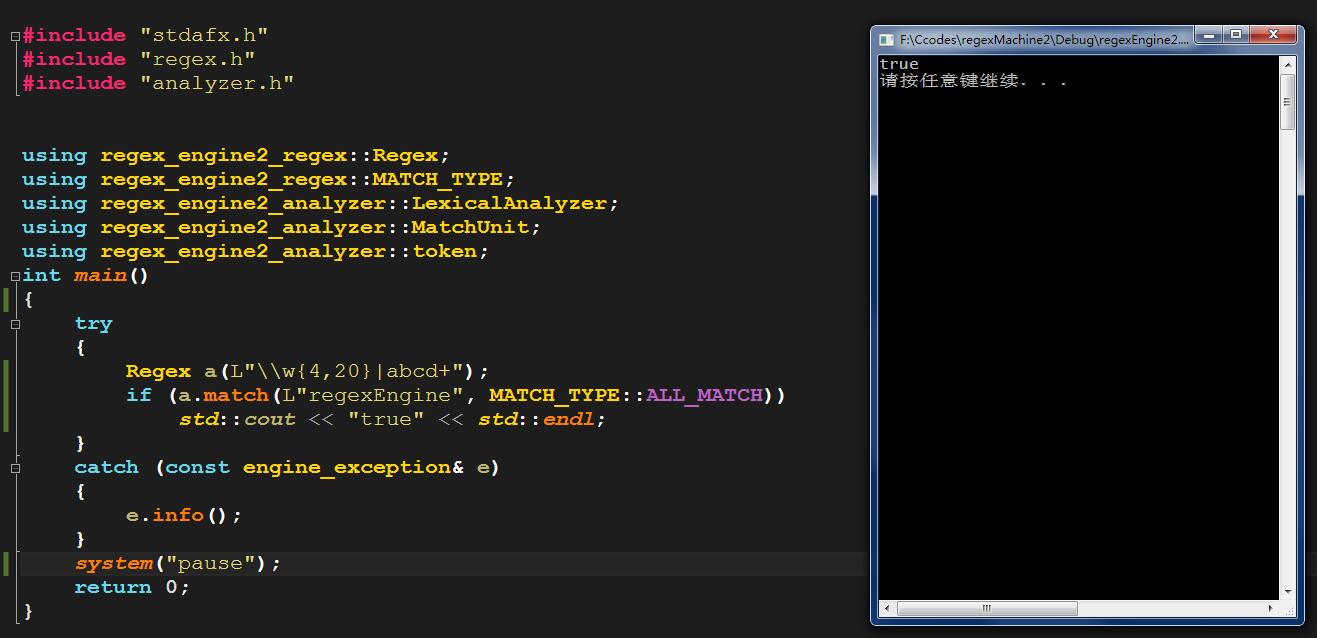
match_example1

图中的match方法的第二个参数为匹配的模式，第一种是ALL_MATCH，第二种是SUB_MATCH，前者将整个给定的字符串作为输入进行匹配，后者会将给定字符串中与表达式匹配的地方筛选出，并存储到result属性中。

同时这一次的实现我也加入了对宽字符的支持：

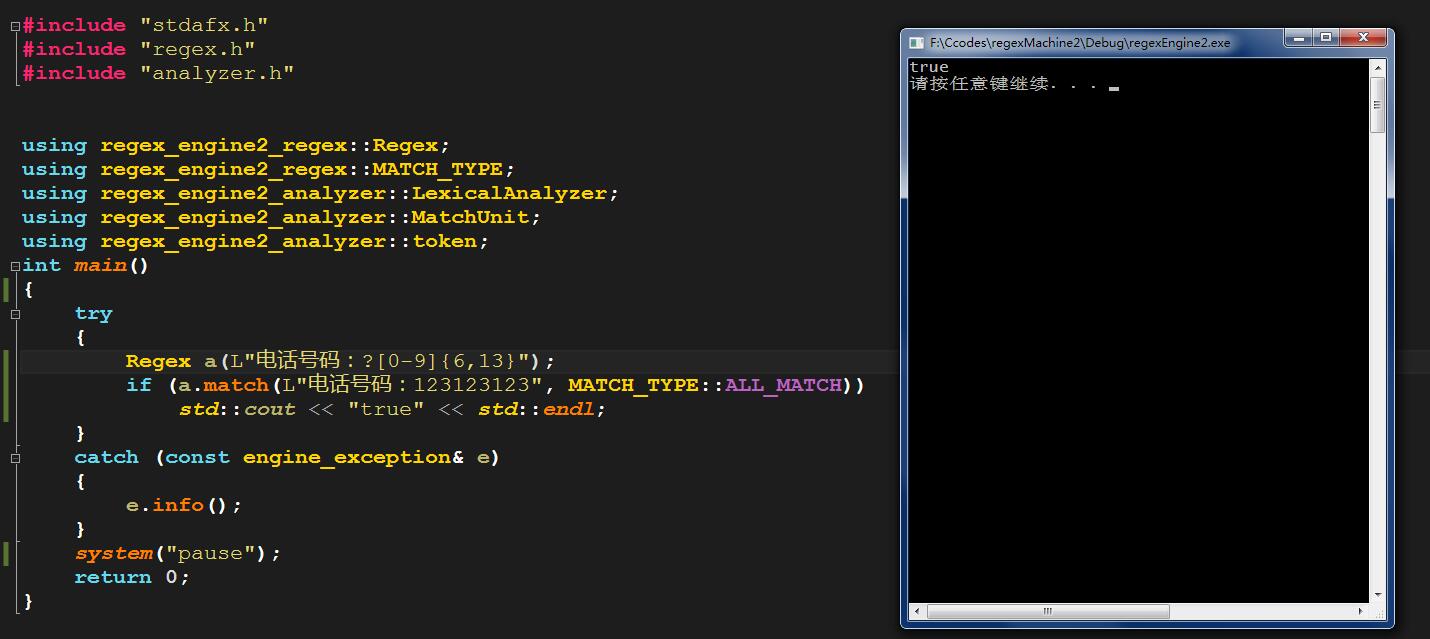
match_example2

最后当书写的正则表达式出现错误时，错误的提示也会更加详细：

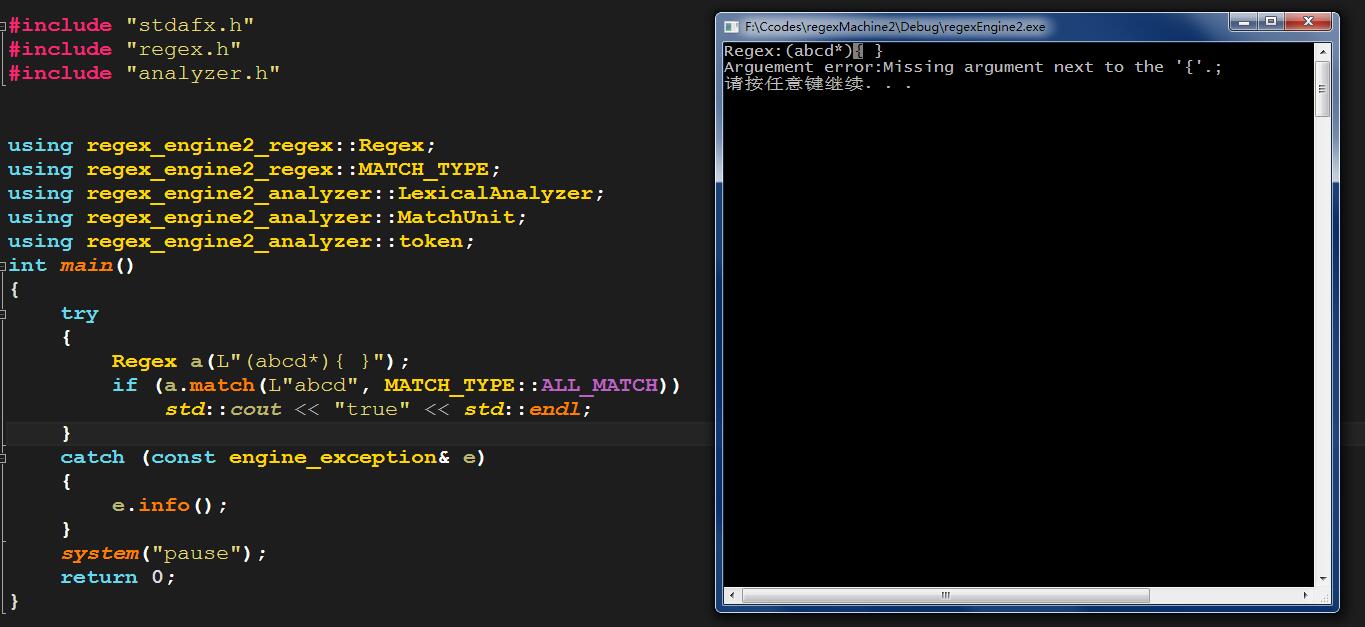
error_example1

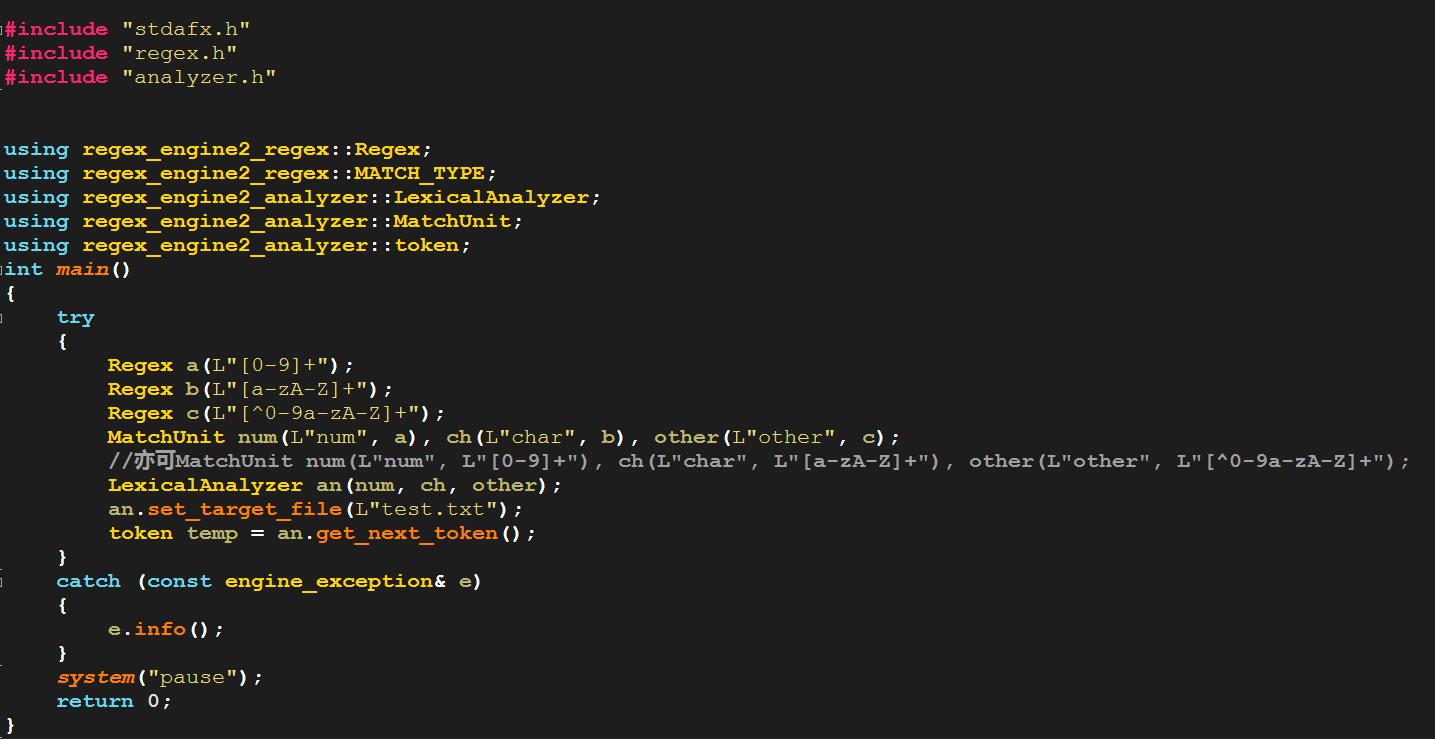
既然正则引擎已经实现了，那顺便实现一个词法分析器的模块也是比较轻松的事情，在头文件analyzer.h文件中定义了两个类，一个是MatchUnit，一个是LexicalAnalyzer，在使用词法分析器的时候，需要实例化MatchUnit类，之后使用MatchUnit的实例来初始化LexicalAnalyzer，在设定好所需要分析的文件之后，便可以通过调用get_next_token方法获取词法单元。

analyzer

实现

　　这一次引擎的实现我采用了业界主流的方法，即首先对正则表达式进行解析，形成抽象语法树，通过抽象语法树得到表达式的字符集以及NFA，通过子集构造法将NFA转换为DFA，最后通过将DFA中的相同状态合并，得到最小化的DFA，这样得到的状态转换表便最终用来进行字符串的匹配。实际上之前的Thompson NFA的实现方法是将正则表达式转换为NFA，之后使用该NFA进行匹配，这种方法实现简单，但是当正则表达式很复杂时，生成的NFA的状态是很多的，这样匹配速度会下降，特别是在重复进行匹配时，时间的消耗很大。而最小化后的DFA状态转换相较于NFA会少了很多的不必要的状态，这样匹配速度会得到大幅提升。接下来我会分别对上述的几个处理过程进行介绍。

解析正则表达式

　　实现的第一步是解析正则表达式，而解析的时候文法是必不可少的，以下是我从网上找到的正则表达式的文法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
RE::= union | simple-RE                 
union::= RE "|" simple-RE               
simple-RE::= concatenation | basic-RE
concatenation::= simple-RE basic-RE
basic-RE::= star | plus | ques | elementary-RE
star::=	elementary-RE "*"
plus::=	elementary-RE "+"
ques::=	elementary-RE "?"
elementary-RE::= group | any | eos | char | set
group::= "(" RE ")"
any::= "."
eos::= "$"  //end of string
char::= any-non-metacharacter | "\" metacharacter
set::= positive-set | negative-set
positive-set::= "[" set-items "]"
negative-set::= "[^" set-items "]"
set-items::= set-item | set-item set-items
set-item::= char-range | char
char-range::= char "-" char

metacharacter: "|" , "." , "*" , "?" , "+" , "[" , "]"
\t {=tab character}
\n {=newline character}
\r {=carriage return character}
\f {=form feed character}
\d {=a digit, [0-9]}
\D {=not a digit, [^0-9]}
\s {=whitespace, [ \t\n\r\f]}
\S {=not a whitespace, [^ \t\n\r\f]}
\w {='word' character, [a-zA-Z0-9_]}
\W {=not a 'word' character, [^a-zA-Z0-9_]}

稍微观察不难发现，该文法是左递归的，同时也没有对{a,b}这个功能的描述，我在解析的时候是采用的递归下降法解析，因此对该文法稍加修改得到：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
RE::= simple-RE union
union::= "|" simple-RE union | ε
simple-RE::= basic-RE concatenation
concatenation::= basic-RE concatenation | ε
basic-RE::= num-range | star | plus | ques | elementary-RE
star::=	elementary-RE "*"
plus::=	elementary-RE "+"
ques::=	elementary-RE "?"
num-range::= elementary-RE "{" range "}"
basic-RE::= elementary-RE special-symbol
special-symbol::= "{" range "}" | "*" | "+" | "?" | ε
range::= num | num "," | num "," num
elementary-RE::= group | any | eos | char | set
group::= "(" RE ")"
any::= "."
eos::= "$"  //end of string
char::= any-non-metacharacter | "\" metacharacter
set::= positive-set | negative-set
positive-set::= "[" set-items "]"
negative-set::= "[^" set-items "]"
set-items::= set-item | set-item set-items
set-item::= char-range | char
char-range::= char "-" char

递归下降解析对文法中的每一个非终结符给出一个处理的函数，层层递归调用，直到遇到文法中的终结符返回，或者是报告一个解析错误，按照上边的文法写出一个针对正则文法的解析过程并不困难。在这里我主要谈一下解析之后生成的抽象语法树的大致结构，在我的工程的regex_ast.h文件中，有对抽象语法树的完整定义，去除一些具体的实现细节，简略的继承关系如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
class IASTNode
{
public:
	virtual void accept_visitor(IVisitor *visitor) = 0;
	virtual ~IASTNode() = default;
};

typedef std::shared_ptr<IASTNode> node_ptr;

class CharNode :public IASTNode
{
public:
	void accept_visitor(IVisitor *visitor) override;
private:
	wchar_t c = -1;
};

class RangeNode :public IASTNode
{
public:
	void accept_visitor(IVisitor *visitor) override;
private:
	node_ptr node;
	int min;
	int max;	//max = -1 means infinity
};

class SetNode :public IASTNode
{
public:
	void accept_visitor(IVisitor *visitor) override;
private:
	std::vector<std::pair<wchar_t, wchar_t>> set;
	bool ispositive = true;
};

class ConcatenationNode :public IASTNode
{
public:
	void accept_visitor(IVisitor *visitor) override;
private:
	node_ptr left;
	node_ptr right;
};

class AlternationNode :public IASTNode
{
public:
	void accept_visitor(IVisitor *visitor) override;
private:
	node_ptr left;
	node_ptr right;
};

class StarNode :public IASTNode
{
public:
	void accept_visitor(IVisitor *visitor) override;
private:
	node_ptr node;
};

class PlusNode :public IASTNode
{
public:
	void accept_visitor(IVisitor *visitor) override;
private:
	node_ptr node;
};

class QuesNode :public IASTNode
{
public:
	void accept_visitor(IVisitor *visitor) override;
private:
	node_ptr node;
};

class EndOfString :public IASTNode
{
public:
	void accept_visitor(IVisitor *visitor) override;
private:
	node_ptr node;
};

可以看到CharNode，RangeNode等类均继承自IASTNode，并重写了父类的accept_visitor虚方法，在这里有必要对该虚方法的产生作说明，在这里我采用了设计模式中的“访问者模式”，当不同的“访问者类”对语法树进行访问时，会调用访问者各自不同的方法，对语法树进行解析，关于访问者模式在网上也有很多的介绍，十分详细，在此不赘述。访问者模式使抽象语法树本身与对抽象语法树的操作相互分离开，使语法树本身更加简洁，同时在扩展对语法树的操作的时候也会更加简便。

字符集

　　字符集顾名思义就是字符的集合，或者说是字符的范围。考虑一下“1|2|3|4|5”这个正则表达式，当我们在构造该正则表达式的NFA或者DFA时，会包含两个状态，一个是初始状态，而另一个是结束状态，而在开始和结束状态之间，会有表示转换的边，当我们没有使用字符集时，我们会在这两个状态之间构造5条边，每条边只匹配一个字符，而当我们引入字符集的概念时，会发现1，2，3，4，5这五个数字其实是相互等价的，我们可以使用1-5这样的范围来表示对这五个字符的匹配，当然，如果使用ASCII码的话，就可以使用61-65来表示。这样初始与结束状态之间就只有一条边了，同样的，当我们在将NFA或者DFA转换为转换表时，表的大小可以进一步缩小，如上边的正则表达式在没有字符集时的转换表应该为：

1 2 3 4 5
状态0 1 1 1 1 1
状态1 -1 -1 -1 -1 -1

在加入字符集后：

1-5
状态0 1
状态1 -1

字符集的引入并不是必要的，但是使用字符集可以使构造出的状态转换更加简单，也可以提高运行时的速度。需要注意的是，字符集的构造其实并不是简单地将相邻的几个字符合并为一个范围项，有时候字符集的构造更多的是一个拆分的过程，考虑这样一个正则表达式：“[0-9]|34”，此时的3，4和其他数字并不是等价的，因此此时的字符集也就并不是简单的0-9，而是需要进行拆分，拆分成为0-2，3，4，5-9，同时从状态转换的角度也可以看出，字符3，4和其它字符的状态转换也是不同的。在我的程序中，字符集的构造是在构造抽象语法树之后进行的，通过遍历一遍语法树，可以构造出该正则表达式的字符集。字符集的详细定义及实现在regex.h文件中。

构造NFA

　　构造NFA的相关方法在网络上有许多相关的资料，在此不赘述，在这里需要注意的是在构造NFA时，我依然使用了访问者模式，构造NFA的访问者类的详细定义见visitor.h文件。在构造NFA时，主要的步骤就是在语法树的每一个节点上调用访问者的方法(在这里是apply方法)，例如在遇到CharNode时，调用的方法如下：

1
2
3
4
5
6
7
8
9
10
11
Automata NFAConstructVisitor::apply(CharNode *n)
{
	status_ptr start = make_shared<NFAStatus>();
	status_ptr end = make_shared<NFAStatus>();
	edge_ptr char_edge = make_shared<Edge>(set.get_group_index({ n->get_char(),n->get_char() }));
	connect(start, end, char_edge);

	record(start);
	record(end);
	return Automata(start, end);
}

首先构造两个NFA状态(start和end)，之后构造一个匹配该字符的边(char_edge)，之后使用该边将两个状态相连即可，其他的结点与此类似，需要注意的是这里的访问者类的方法有一个返回值，而一般的对访问者模式的介绍中并没有介绍带返回值的情况，而带返回值的方法主要是为了解决在解析正则表达式中{a,b}这个功能(在我的实现中，使用这个功能的结点被命名为RangeNode)时遇到的问题(在这里要感谢vczh的项目源代码，给了我莫大的帮助)，这个结点在构造NFA时，需要将这个结点的子节点重复构造多次，每一次构造出的NFA片段都是相同的，而如果apply的方法不带返回值，则难以对这个结点进行解析，而如果带有返回值的话，就可以采用递归调用的方式，重复地构造NFA片段，因此针对RangeNode的方法可以这样写：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
Automata NFAConstructVisitor::apply(RangeNode *n)
{
	Automata head;
	int min = n->get_range().first, max = n->get_range().second;
	if (min == 0 && max == -1)
	{
		auto start = make_shared<NFAStatus>();
		record(start);
		auto frag = invoke(n->get_node());
		auto end = make_shared<NFAStatus>();
		connect(frag.end, frag.start);
		connect(frag.end, end);

		connect(start, frag.start);
		connect(start, end);

		record(end);
		return Automata(start, end);
	}
   ......
}

其中的frag = invoke(n->get_node())便是对其子节点解析的过程，解析得到的返回值，便是子节点所构成的NFA片段。当使用带返回值的访问者模式时，其访问者类的定义和不带返回值的访问者类会稍有不同，在visitor.h文件中，对构造NFA的访问者类NFAConstructVisitor有如下的定义：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
class NFAConstructVisitor :public IVisitor
{
public:
	NFAConstructVisitor() = delete;
	NFAConstructVisitor(CharSet e) :set(std::move(e)) {}
	Automata invoke(node_ptr n) {
		n->accept_visitor(this);
		return NFA;
	}
	void visit(CharNode *n) override {
		NFA = apply(n);
	}
	void visit(ConcatenationNode *n) override {
		NFA = apply(n);
	}
	void visit(RangeNode *n) override {
		NFA = apply(n);
	}
	void visit(SetNode *n) override {
		NFA = apply(n);
	}
	void visit(AlternationNode *n) override {
		NFA = apply(n);
	}
	void visit(StarNode *n) override {
		NFA = apply(n);
	}
	void visit(PlusNode *n) override {
		NFA = apply(n);
	}
	void visit(QuesNode *n) override {
		NFA = apply(n);
	}
	void visit(EndOfString *end) override {
		NFA = apply(end);
	}
	Automata apply(CharNode*);
	Automata apply(ConcatenationNode*);
	Automata apply(RangeNode*);
	Automata apply(SetNode*);
	Automata apply(AlternationNode*);
	Automata apply(StarNode*);
	Automata apply(PlusNode*);
	Automata apply(QuesNode*);
	Automata apply(EndOfString*);
private:
	Automata connect(Automata &, status_ptr &);
	void connect(status_ptr &, status_ptr &, edge_ptr);
	Automata connect(Automata &, Automata &);
	CharSet set;
	Automata NFA;
};

通常的访问者模式是由被访问的元素调用accept_visitor方法来进行访问的，但是在构造NFA时，是使用NFAConstructVisitor的实例在语法树的根节点调用invoke方法进行解析的，之后程序会顺着根节点向下进行一次深度遍历，在遇到不同的节点类型时，不同的visit方法和apply方法会被调用，而其中的私有属性NFA作为解析后得到的NFA片段的一个暂存，最后会作为返回值，在invoke结束之前被返回，整个的解析过程配合着visitor.cpp中的具体实现来看会更容易理解。整个调用的过程比较复杂，但是如果对面向对象语言的多态性以及动态类型静态类型有比较好的理解的话，相信理解访问者模式和上边的代码也不太困难。

构造DFA

　　构造DFA时我使用的是子集构造法，子集构造法有三个重要的操作：

操作 描述
ε-closure(s) 能够从NFA的状态s开始只通过ε转换到达的状态集合
ε-closure(T) 能够从集合T中某个NFA状态s开始只通过ε转换到达的NFA状态集合
move(T,a) 能够从T中某个状态s出发通过标号为a的转换到达的NFA状态的集合

ε转换指的便是我们在构造NFA时大量使用的空边，空边是不匹配任何字符的，一个状态可以在没有读入任何字符的状态下通过空边进入另一个状态，而这两个通过空边相连的状态实际上是可以合并的，通过这样的合并有时可以(但并没有理论说明一定会)减少状态机中的状态数目，同时消除空边。而子集构造法便是通过将这些可以合并的状态合并成为一个状态构造出DFA的。子集构造法的算法如下，其中的s0表示开始状态：

1
2
3
4
5
6
7
8
9
10
//一开始，ε-closure(s0)是Dstates中的唯一状态，且它未加标记；
while(在Dstates中有一个未标记状态T){
  给T加上标记;
  for(每个输入符号a){
    U = ε-closure(move(T,a));
    if(U不在Dstates中)
      将U加入到Dstates中，且不加标记;
    Dtran[T,a] = U;
  }
}

　　实际上在我的实现中，从NFA转换得到的DFA就已经是状态转换表的形式了，每一个DFA状态的实例中都会包含一个status_tran的私有变量，该变量记录了在不同的输入字符上的状态转换。当把所有的这些DFA状态集合到一起，就构成了一个完整的DFA状态转换表。

最小化DFA

　　实际上构造出的DFA也可以用来进行字符串的匹配了，在多数情况下，相较于NFA，DFA的状态数目会大大减少了，但是即便如此，DFA依然有进一步简化的余地，就以龙书上的例子进行说明，正则表达式“(a|b)*abb”的DFA转换表如下：

DFA状态 a b
A B C
B B D
C B C
D B E
E B C

观察这个转换表我们可以发现，状态A，C，E的状态转换是相同的，我们可以考虑是否可以像构造DFA时一样将这些状态合并成为一个状态，从而进一步减少状态的数量，实际上这是可行的，但是并不是A，C，E都合并到一起，而是将A，C合并到一起，因为E状态是结束状态，因此E状态与A，C状态本质上是不同的。实际上，我们还有更加严谨的方法来检验两个状态是否是可以合并的，在这里我们就要引入区分的概念：如果分别从状态s和t出发，沿着标号为x的路径(这里的路径可能包含多个字符)到达的两个状态中只有一个是接受状态(即结束状态)，我们说串x区分状态s和t，这样状态s和t就是可区分的，如果找不到这样的路径，那这两个状态就是不可区分的。上边的状态A和C就是这样的两个状态。因此最小化DFA的过程是一个不断分组的过程，我们把一个集合中可区分的状态全部摘除出去，最后剩下的就是不可区分的状态，同时也就是可以合并的状态。需要注意的是，结束状态和非结束状态在一开始就是分离的，不可合并的。但需要注意的是在实际的使用中，我们并不直接使用区分的定义去合并DFA的状态，因为定义中的路径是不定长度的，同时到达状态是否是结束状态的限制也比较大，因此状态最小化算法依据的实际上是区分的等价变形，最开始我们将DFA的状态划分为结束状态组和非结束状态组，我们选定某一个输入符号a，检查每一个组中的某两个状态在a上的转换，如果它们的转换都到达同一个组的状态，那这就可以说明符号a不能区分这两个状态，我们重复这个过程，检查这两个状态在其他符号上的转换，看是否有其他符号能区分这两个状态，如果能，则包含这两个状态的组需要进行拆分。同时也要对每一分组中的状态两两检查，直到使得两个状态s和t在同一小组中当且仅当对于所有的输入符号，这两个状态的转换都到达同一个组，或者更简单的方法是检查分组的数量有没有变化。这样就完成了状态的最小化。

　　让我们用这一算法来最小化一个稍微复杂一点的正则表达式“(123?){2,5}|(abc*){4,6}”，运行后得到的NFA，DFA和最小化DFA的结果如下：

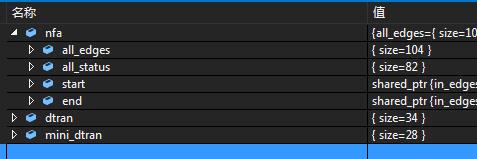
result

可以看到，解析之后得到的NFA的状态数为82，DFA的状态数为34，最小化DFA的状态数为28，当正则表达式更加复杂时，状态的缩减还会更加明显。

　　有趣的是，子集构造法并不总是会将NFA的状态数减少，例如正则表达式“(a+b?){5,10}”，它的构造结果如下：

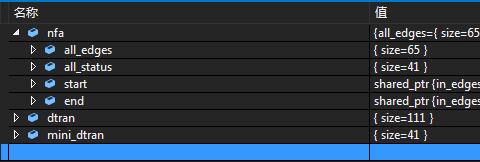
result2

可以看到NFA的状态数为41，而DFA却达到了111，最小化后依然为41，这应该算是构造时候的一种比较特殊的情况。

总结

　　总结没什么可说的，这个项目总的来说花的时间比较长，最终的实现也有一些小的瑕疵，例如最小化DFA的算法写得效率并不高，状态数量太多的话运行速度会很慢。不过也还算是有收获，然后是时候把编译原理向前推进一下了。